Formula For Calculating Volume Chemistry

Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships , then put them together in the ideal gas law. The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law). The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law).

Formula For Finding Volume Chemistry Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). When products or reactants are gaseous in form at standard temperature and pressure, the molar volume of a gas and mole ratios can be used to convert the volume of one substance to moles of another substance. One mole of an ideal gas has a volume of 22.4 L at standard temperature and pressure. Molality is an intensive property of solutions, and it is calculated as the moles of a solute divided by the kilograms of the solvent.

Unlike molarity, which depends on the volume of the solution, molality depends only on the mass of the solvent. Since volume is subject to variation due to temperature and pressure, molarity also varies by temperature and pressure. In some cases, using weight is an advantage because mass does not vary with ambient conditions. For example, molality is used when working with a range of temperatures. To have value, measurement results must be metrologically traceable to an appropriate reference, which in the cases treated in this chapter are SI units of mass, volume, and amount of substance. A statement of measurement uncertainty always accompanies a traceable result.

Methods must be validated and verified for use by a particular operator at a particular time. Accreditation to an appropriate standard, such as ISO , is overseen by organisations usually with governmental or quasi-governmental status. Gaining accreditation for a particular method shows that a laboratory is using validated methods by competent personnel, but of course can never guarantee a reliable result . In this section we will review the components of measurement uncertainty of mass and volume measurements and then apply this to the preparation of a standard solution and a typical titration. It is noted that the metrological traceability chain will involve multiple branches , often through amount fraction or mass fraction. For more information, see the chapter on quality assurance in the forthcoming 4th edition of the Orange Book , or in .

For more accurate measurements, glassware that has been certified by standards agencies may be purchased. Alternatively, one can calibrate glassware to an accuracy generally as good as the standards specifications, correcting for weight in vacuum, glassware expansion or contraction, and water expansion or contraction. Table 3.2-2 lists the calculated volumes for one gram of water in air at atmospheric pressure at sea level for different temperatures, corrected for buoyancy with stainless steel weights of density 7.8 kg m−3. The glass volumes are also calculated for the standard temperature of 20 °C, with small adjustments for borosilicate glass expansion or contraction with temperature changes. Volume is the quantification of the three-dimensional space a substance occupies.

By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight.

This calculator computes volumes for some of the most common simple shapes. Is the volume occupied by one mole of a chemical element or a chemical compound. It can be calculated by dividing the molar mass by mass density (ρ). Molar gas volume is one mole of any gas at a specific temperature and pressure has a fixed volume. Calculations involving the mole can be used to determine unknown concentrations, volumes and masses in reactions. One mole of any gas occupies 24 cubic decimetres at room temperature and pressure.

Gases whose properties of P, V, and T are accurately described by the ideal gas law are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter. Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures. To calculate the molarity of a solution, the number of moles of solute must be divided by the total liters of solution produced. If the amount of solute is given in grams, we must first calculate the number of moles of solute using the solute's molar mass, then calculate the molarity using the number of moles and total volume.

Transition potential is often given instead of the formal redox potential. It corresponds to the colour change at which the end-point is said to occur. It is a function of the formal redox potential, the total concentration of the indicator , the depth of the colour layer, the minimal observable absorbance , and the absorption coefficient. In an ideal two-colour indicator, the "apparent absorption coefficients" of both forms should be equal.

Then the transition potential approaches the formal one. As for formal redox potential, it should be given, at least for the acidity range of indicator application. The transition potential may be given for pseudo-reversible indicators.

Because the transition point is usually different for oxidimetric and reductiometric titrations, it is sometimes useful to distinguish those two values. The interest stems from that accurate measurements of the unit cell volume, atomic weight and mass density of a pure crystalline solid provide a direct determination of the Avogadro constant. Specific volume is defined as the number of cubic meters occupied by one kilogram of matter. It is the ratio of a material's volume to its mass, which is the same as the reciprocal of its density. In other words, specific volume is inversely proportional to density.

Specific volume may be calculated or measured for any state of matter, but it is most often used in calculations involving gases. Compared to molar concentration or mass concentration, the preparation of a solution of a given molality is easy because it requires only a good scale; both solvent and solute are massed, rather than measured by volume. Molar volume of gases One mole of gas occupies \(\text\) \(\text$\) at standard temperature and pressure.

The most common molar volume is the molar volume of an ideal gas at standard temperature and pressure (273 K and 1.00 atm). End-point error – the systematic error occurring because the equivalence-point potential differs from the end-point potential under the given conditions of titration. The equivalence-point potential depends on the formal potentials of the analyte and titrant and on the number of electrons participating in half-reactions.

When the transition potential, corresponding to the end-point, is close to the equivalence-point potential, the effect of the above-mentioned factors may be diminished. 1 mole of an ideal gas occupies a specific volume at a particular temperature and pressure. The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional. Charles's law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant. Examples and practice problems of solving equation stoichiometry questions with gases.

We calculate moles with 22.4 L at STP, and use molar mass and mole ratios to figure out how many products or reactants we have. Similar terms apply to complexometry , oxidation-reduction, and precipitation titrimetry. In the last case, substances which are adsorbed or desorbed, with concomitant colour changes at or near the equivalence-point, are termed adsorption indicators.

It is usually expressed in terms of the negative decadic logarithm of the concentration (e.g. pH, pM) or, for oxidation-reduction titrations, in terms of a potential difference. Standard solutions are often prepared by dissolving an accurately measured mass of a solute of certified purity in a known volume of solvent. If the concentration of an intended standard solution is obtained by measurement, for example by titration with a standard solution, it is known as a secondary standard [VIM 5.5]. The measurement of mass is a central point of the quantification of material substances.

A balance measures mass by sensing the weight force that presses an object down on the balance pan. Weight is the force exerted on a body by the gravitational field of the earth, and is measured in the unit force newton, N. The weight force acting on 1 kg mass depends on geographic and cosmic factors.

However, for mass measurements using mechanical balances, the weight of the unknown object is equilibrated at the same place and same time as the weight of an object of known mass (i.e. of a standard). For high precision measurements, the buoyancy caused by the surrounding air must be taken into consideration. This correction can easily be calculated if the density of the known and unknown mass and that of the air is known.

Two solutions that have the same molarity will have the same number of molecules of the chemical per liter but are likely to contain differing masses of that chemical per liter to achieve this. Whereas two solutions at the same concentration will have the same mass of the chemical per liter of solution but are therefore likely to have differing numbers of molecules of that chemical per liter. Provided some additional information is known, one value can be deduced from the other using the equations below. This means equal amounts of moles of gases occupy the same volume under the same conditions of temperature and pressure. This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 9.11.

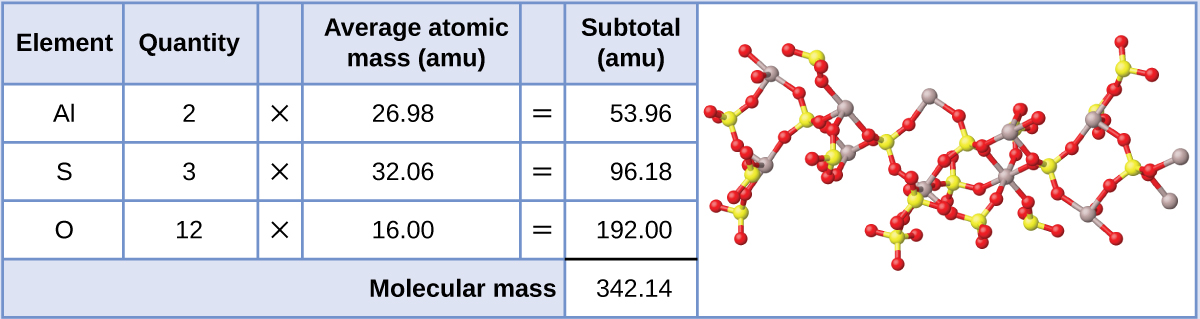
Add the atomic masses of the solute together to find the molar mass. Look at the elements in the chemical formula for the solute you're using. List the atomic mass for each element in the solute since atomic and molar mass are the same.

Add together the atomic masses from your solute to find the total molar mass. In a mixture of ideal gases, the mole fraction can be expressed as the ratio of partial pressure to total pressure of the mixture. The relative formula mass of a compound is calculated by adding together the relative atomic mass values for all the atoms in its formula. In fact, gravimetric analysis was used to determine the atomic masses of many elements to six-figure accuracy. The relationship among the moles of a gas, the volume of the gas in liters, and the molar volume is similar to the mass-to-mass formula. A small teaspoon of sodium hydrogencarbonate weighs 4.2g.

Calculate the moles, mass and volume of carbon dioxide formed when it is thermally decomposed in the oven. Assume room temperature for the purpose of the calculation. This relationship shows us that the only way to increase the volume of gas, V, while maintaining the same temperature and pressure, is to increase the moles of gas, n, that are present, that is, add more gas. This relationship shows us that if we increase the moles of gas, n, by adding more gas while maintaining the same temperature and pressure, the volume of gas, V, will also increase. A typical solution is made by dissolving some solid substance in a liquid. The amount of substance that is dissolved in a given volume of liquid is known as the concentration of the liquid.

Mathematically, concentration (\(c\)) is defined as moles of solute (\(n\)) per unit volume (\(V\)) of solution. Water hardness, the concentration of titratable calcium and magnesium, is measured by complexiometric titration using the blue dye Eriochrome Black T as the indicator. When added to water, the indicator reacts with Ca2+ and Mg2+, exhibiting a wine-red colour. Upon reaction with the titrant EDTA the colour becomes blue.

Water hardness is expressed as an amount concentration of calcium and magnesium or an equivalent mass concentration of calcium carbonate or calcium oxide. Formal redox potential corresponds to the redox potential in solution at which the analytical concentrations of the reduced and oxidised forms of the indicator are equal. This should not depend on the concentration of the indicator, unless the stoichiometric coefficients are not equal.

In such instances the formal redox potential should be replaced by the half-oxidation potential. The formal redox potential is a function of ionic strength and acidity and its value should be given under the specified conditions in which it is used for determinations. The formal redox potential should be given, at least for the acidity range in which the indicator is applicable.

The formal redox potential has a precise meaning only for strictly reversible indicators. In the case of other indicators, it should be understood as the potential for half-oxidised indicator. This borderline concentration level should approach as closely as possible the concentration of the free metal aquo ion at the equivalence-point of a particular titration reaction.

The change of the optical property extends over a range of metal aquo ion concentrations, which is often termed the transition range. Systematic error arising from the reaction of the indictor with H+ (in acid-base titrations) or metal ion . This error has a negative value and depends on the amount of indicator present. For indicators exhibiting high colour intensities, which therefore may be used in smaller concentrations, this error decreases. A significant compensation of this error usually takes place, because the standardisation of the titrant is carried out in similar conditions to the analysis titration. For example, phenolphthalein (colour change between pH 8.2–10.0) should not be used for a strong acid-strong base titration with an equivalence-point of pH 7.0.

Values for atomic and therefore molecular masses are normally obtained relative to the mass of the isotope 12C (carbon-12), however "relative" is generally omitted from the title. And even to estimate molecular weights, and there are many reports of such studies in the literature, as highlighted in the following section. In particular we could demonstrate that frequency shifts describing the intermolecular interactions between anions and cations in ILs can be dissected into reduced mass and pure interaction effects. The equation is read as 1 mole of calcium atoms reacts with 2 moles of hydrochloric acid to form 1 mole of calcium chloride salt and 1 mole of hydrogen gas molecules . Likewise, the only way to decrease the volume of gas, V, while maintaining the same temperature and pressure, is to decrease the moles of gas, n, that are present, that is, remove some of the gas.

Likewise, if we decrease the moles of gas, n, by removing some of the gas while maintaining the same temperature and pressure, the volume of gas, V, will also decrease. Molar volume of ideal gas, Vm, is defined as the volume of 1 mole of the ideal gas at a specified temperature and pressure. To calculate the concentration of a solution, start by converting the solute, or the substance being dissolved, into grams. If you're converting from milliliters, you may need to look up the solute's density and then multiply that by the volume to convert to grams. Finally, divide the solvent by the solute to find the concentration of the solution. (Add the atomic masses of the constituent elements.) Then, convert milligrams to grams by dividing by 1000.

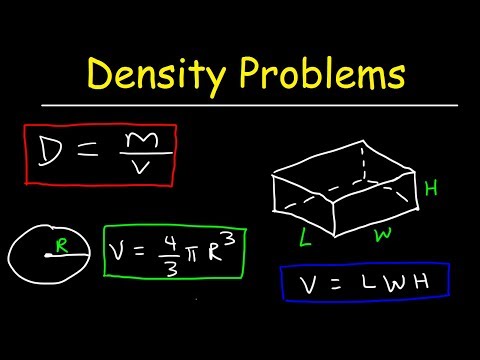
Finally, divide the grams of your substance by the Molar Mass. The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises. Of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m3).

How Much Does It Cost To Fix Paint Chips On Car

When you want perfect, showroom-finish results, full professional car scratch repair is the way to go. Both car dealerships and auto body shops can do this for you. Some of the other car scratch repair options that professionals may offer include the use of rubbing compounds, car scratch repair kits, touchup paint, and airbrushing. These scratches should be repaired immediately, as exposed metal can rust if exposed to the elements long enough.

If the scratch appears silver, it has likely hit the metal underneath the clear coat, paint, and primer. These types of scratches are the most expensive to repair, with auto body shops charging anywhere from $800 to $1,500 on average for deep paint scratch repair. In situations where car scratch repair has to be done on multiple sections or the entire car, auto insurance can save you a lot of money. Also worth noting is that when you file a claim for scratch repair, you'll have to pay your deductible, which may be a significant amount. Therefore, it's also wise to first establish how much it would cost to repair the scratches outside your insurance before you file a claim.

You could just skip repairing an auto scratch, but rust and ugly paint damage are probably things you want to avoid! An auto scratch repair service at an auto body shop can be very expensive, so we recommend doing it yourself with touch up paint. In this article we will show you how to fix your auto scratches with great results at the lowest cost possible. All car scratch repair pens are marketed as an effective, easy and inexpensive remedy for clear coat scratches. Supposedly, they should also work on all car paint colors.

The professional results provided by these pens, they say, will save you from a very costly bill at an auto body shop. It's always unfortunate getting into accidents because most of the time it's not our fault. Bumper scratches, chipped paint are the most common problems when a car accident occurs and they can also be the most expensive. Depending on how severe the scratches and scuff marks are, professional repair costs range from 150 to $600 per panel, depending on if the panel is fixable or not. This will heavily depend on the integrity of the body shop repairman which many have reported to be ripped off on unfixable jobs.

Many businesses are now known to purchase fake yelp and google reviews in order to trick people into doing business with them. A car accident is never fun, either is the resulting damage and paying for car repair costs. If you've dented your bumper, developed deep paint scratches or otherwise damaged your car, you may be surprised to discover how much does body work cost.

The car repair cost for auto body mishaps can range between $50 to $1,500, and more. Just about any body shop can handle car paint chip repairs, there are also mobile repair businesses that come to you. The cost of repair through one of these options is generally between $35 and $85 with an average cost of $50.

You can get a quote ahead of time and compare the cost, quality and service before deciding which way to go. Body shops will also help in estimating and repairing chips that have began to rust. The car paint chip repair cost will vary with the size of the chip and its location on the vehicle.

Scuffs may be harder to spot than deeper scratches because there is no change in color from the scratch. This depth of scratch can usually be repaired by hand buffing or polishing. Scratch Wizard estimates auto body shops charge less than $100 on average to repair scuffs. Depending on the damage, you might be required to make payments out of pocket, from as little as $50 to thousands of dollars. In fact, estimates for car paint repair costs can range from $150 for minor scratches to $7,500 or more for showroom-quality paint jobs.

You could also save money on damaged car paint or scratches by doing the repairs yourself. Avoid the potentially higher price tags of dealerships and body shops by buying rubbing compounds and touch-up paint pens at a lower cost. Clean the car paint chip to begin paint chip repair with soap and water and then dry it with a soft cotton cloth. Rub a dab of automotive polishing compound over the paint chip to gently soften any ragged edges.

If your car has relatively small scratches or scuffs , a touch up paint pen is the easiest and cheapest product to use. It has a felt tip which when depressed releases small amounts of auto paint. It really helps to practice with the paint pen before using it on your automobile.

A smooth surface like a photograph or plastic container will help you get a feel for how the auto paint flows from the pen tip. When you are ready, make sure the scratched areas are clean and primed if necessary. Apply several thin layers with the auto scratch repair pen, letting each dry before applying the next.

Finish with a couple clearcoat layers and polish with rubbing compound for a glossy finish. Our team will help you find the lowest insurance prices. The cost to repair the scratches on your vehicle depends on how numerous and deep they are. A surface scratch can cost you as little as $150, but a deep paint scratch can cost upwards of $2,500. The average cost of a full car scratch repair is around $3,500.

Auto body shops specialize in car body panel repair, and so they offer more experience and expertise in car scratch repair. They're also likely to have more than one method of repairing the scratches. A chip in your car paint doesn't have to be detrimental, there are solutions to repair the paint chip.

You can choose to work with a professional body shop or repair the chipped paint at home. There are kits to work with at home and if you decide a professional is the way to go costs to consider. You should always check with your automobile insurance before you proceed to see if the repair is covered.

If you decide to buy the sandpaper, paint, primer, and clear coat and do all the work yourself, you may end up spending between $600 and $1,500. If you enlist the services of professional mechanics, you'll likely end up paying anywhere from $1,500 to $2,500. Here are some of the most frequently asked questions before seeking professional scratch repair services that will save you money time and frustration.

Bear in mind that many DIY scratch fixes are not the final solution for all situations. This is a typical rock chip that you can fix with this procedure. In fact, even if the chip is about one-fourth the size of a dime, you can still repair it. Clean the chip with soap and water and then dry it with a soft cotton cloth. Rub a dab of automotive polishing compound over the chip to gently soften any ragged edges. Too much rubbing could damage the clearcoat over the paint and make a cloudy mess.

There's nothing more annoying than scratching your car. We have over 60,000 colours to match any paint work you have. Our highly experienced and professional team will come to you and fix any car scratches you have. We also repairchipsand dents, and can applypaint protectionso you don't have to worry about your paint getting damaged again. Call us today and see the difference professional scratch repair can make for your vehicle. A mark that has more deeply scratched clear coat is a little more difficult to repair, but not by much.

These scratches can be polished down until they are almost invisible, but never fully removed. These types of scratches also usually cost less than $100 for professional repair at an auto body shop. Another costly part is a complete repaint of the car bumper. The average costs of painting a car bumper are around $500-$600. If you are not satisfied with the cheaper price you could always go to a professional auto body shop which will probably charge around $1,000 for the job. Ultimately, the cost of car scratch repair depends on the severity of the car scratches.

Investing in car wax, a paint sealant, or a ceramic coating will also go a long way in helping to keep your car's surface scratch-free. You will require collision coverage to repair dented bumper, suspension damage and rear-end damage. Whereas you will need comprehensive coverage for deep paint scratches and a cracked windshield.

Unlike a full respray, paint touch up only targets a specific area, thus minimizing the size and cost of the repair. We start off by repairing your vehicle by covering all areas in the vicinity of the repair, including your wheels. Our preparation process ensures optimal adhesion of the paint for a quality finish. Depending on how your paint was chipped it may be covered under your car insurance policy. If it was as a result of an accident, weather conditions or vandalism you may be covered.

Always document damage when it occurs or you notice it first. Most insurance companies will ask you to acquire repair quotes from a number of different body shops before you're able to process the claim. Some insurance companies have a list of approved body shops they work directly with. The cost can easily skyrocket up to $7,000 if you drive a luxury vehicle or are looking for a top of the line paint job.

Thankfully no dents but there are several stone chips and key scratches on the car. I really want the car fixed up like it just came out of the dealership. The major problems are the paint chips and the parts that are showing metal/primer. All of this protection helps to maintain the resale value of your car and keep your ride looking sexy and pristine for years to come. It can feel unfair to be stuck with the cost of car paint repairs after insurance won't foot the bill.

However, it's important to keep in mind that most of the time, car paint damage isn't essential to the functionality of your car. So while you may be able to take out a loan or charge a credit card in order to pay for these repairs, it may be better to save up and budget in advance. Having car insurance can save you a bundle when you're getting paint repaired. When it comes to repairing car paint, some things are covered under insurance while others are not. In general, if you have comprehensive insurance coverage, it's likely that the repair will be covered.

There are many factors that can influence these car scratch repair costs, including the type of car you have, the extent of the damage and how you choose to pay for it. Paint chips can take away from the look of a vehicle while decreasing value. Our technicians utilize an advanced paint chip repair process. Technicians are able to eliminate a large quantity of small paint chips and scratches concentrated in one area without sanding and repainting the vehicle.

It is tempting to cut the visit to the body shop and save money doing car paint chip repairs at home. However, there are cases where this can do more harm than good. If you have any of the following, just go to a professional and DO NOT do it at home.

The last thing you want is to be paying for car repairs out-of-pocket when you thought the auto insurance would cover those costs. We've got a simple guide to get you started on what auto body repairs are covered by your car insurance. If you get scratches and paint chips straight out of the dealership, the dealership will most likely decline to do any fixing.

However, if you've bought it with chipped paint, the dealership could be liable to provide for repairs. In this case, they'll contract the repair to a professional detailer. In most cases, you'll have to prove there were scratches and paint chips before you've bought the car. The price also ranges on how deep the scratch is and if it is has penetrated the primer. Usually, you can save yourself the money and time by getting yourself your very own car scratch repair Kit. You're only taking a few minutes for you to rub out the nasty scratches on your quarter panels or bumper bar.

To fix paint chips, you will need touch-up kits, these can be easily obtained at your dealership or auto-shop near you. These kits usually contain a clear coat, sanding tools, rubbing compound, color-matched paint that looks exactly like that of your factory color, and a primer. There are few things more frustrating and concerning than spending thousands of dollars on vehicle maintenance only to have your car's look ruined with a scratch. Even a tiny scratch can ruin the look of an otherwise beautiful paint job, especially if it's on a very noticeable spot or the rest of your vehicle is otherwise pristine. The good news is that no scratch is too hard to repair; the bad news is that scratch repair can be quite expensive depending on the location and size of the damage.

In those situations where your car's scratches have to be attended to by professionals, you can either take your car to your local car dealership or an auto body shop. Many people opt for auto body shops because they're often cheaper, and also because they're likely to give the scratches on your car more detailed repair. Reverse is the newest car detailing product that easily removes scratches and swirls by hand. This car scratch remover and car paint scratch repair compound will bring your paint back to new. Make paint correction easy with this all in one formula.

How to fix stone paint chips on your car Clean the area with soap and water, then rub down with alcohol or white spirit. Once the paint is dry, sand gently to make it the same level as the surrounding paint. If you have the right policy, your insurance pays for your scratch repairs, not you. If your scratch results from a collision, you or the other driver needs collision insurance depending on who is at fault.